From a developers perspective, a software synthesizer is never fast enough. More speed means more CPU cycles to throw at making it sound better, means more processing possibilities on the sound.

Eventually, almost every beginning softsynth programmer will fall into the trap of thinking that SIMD parallelization (e.g. using SSE instructions) offers a silver bullet; yielding speedups in to 200-400% range. Let me just pop that bubble right away: you might get a bit of a speedup, but it’ll be a lot lower than that. Seriously - if you get 50% speedup, you’ve done very well. Audio code is just not that well suited to SIMD parallelization.

However, SSE is still worth using, even with the added complexity it brings to your synth. Let me explain why.

5 questions

Here are five more or less related questions, that you might ask yourself when working out the computational side of a software synthesizer.

How will you handle denormals?

Individual samples should be represented as floating point numbers in your synth, because that is absolutely the simplest way to do it.

Without getting into too much detail, floating point numbers can’t represent every number in the universe (although they try), because they have a limited number of bits to do so. That means that there is a limit to how big a number they can represent, and a how small a number they can represent.

In that space between zero and the smallest representable number, an ungodly abomination exist: denormals. Denormals are an alternative number representation which kicks in when numbers become smaller than the smallest representable number in the usual representation. And they’re slow. Horribly slow. Completely unusable.

Denormals happen to everybody, they’re just a fact of life in a softsynth. Denormals usually result from exponential decay, that is, repeatedly multiplying a number by something smaller than 1. This will get you into denormal territory faster than you’d think. Exponential decay is an integral part of softsynths, occurring in envelopes, filter, reverbs, delays and more. So you have to handle denormals.

There are different ways to handle denormals. Laurent De Soras has written an excellent article with a number of solutions.

Should computation be done in 32-bit or 64-bit floats?

Here we hit a simplicity vs. performance tradeoff. It is simpler, and therefore preferable, to use 64-bit floats. It is faster, and therefore preferable, to use 32-bit float.

In 32-bit floats, you only have 24 significant binary digits. That is not a lot, and it’s certainly not enough to avoid numerical stability headaches in highly recursive structures like deep IIR filters. It can also cause you problems with accurately representing phase if (for instance), you’re using big wavetables. And rather than switching back and forth between representations, it would be simpler to just use the same representation everywhere.

The performance hit here is not on the CPU; 64-bit computations are going to be about as fast as 32-bit ones. The problem is memory bandwidth, and specifically, cache trashing. You have to be extra careful with your memory usage patterns if you’re using 64-bit floats.¹

Should computations be done using the FPU or SSE?

This is a complicated question, and the answer is that it depends, of course. If you can exploit the SIMD possibilities of SSE, it is probably a good idea to do so. If you can’t, whether you do your computation in SSE or on the FPU is not going to matter a whole lot. Except for one little advantage SSE has, which we’ll cover later.

What should your strategy be for SSE parallelization?

If you we’re going to use SSE, you would have to think about what your strategy would be for parallelization. One very intuitive idea is to parallelize over time, computing 4 consecutive 32-bit samples in the stream at the time, like this:

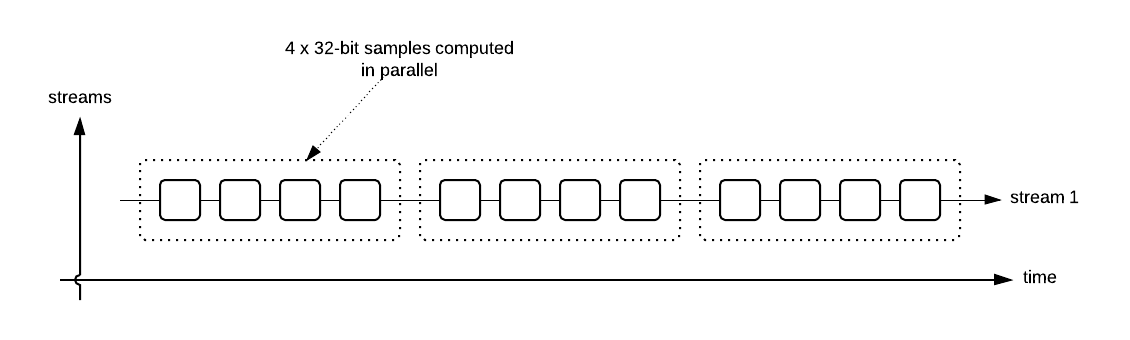
This could potentially be very efficient! The problem is that most algorithms you’re writing don’t really lend themselves to this structure, because samples depends on previous samples, and you’re computing those at the same time, so they’re not available yet. This is the case in IIR filters and delay-based effects, which make up quite a significant part of your synth.

Another approach is to parallelize in the other direction: a single sample over multiple streams, like this:

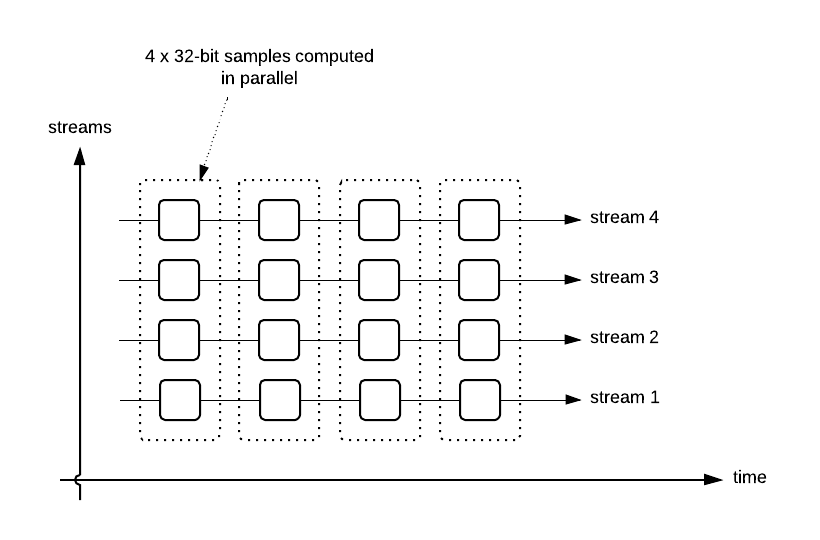
So for instance, if you had a one-pole filter, you could run that filter on 4 streams simoultaneously, only moving forward one sample at the time. This is potentially a good idea, but in practice it becomes unwieldy. The logic for choosing which streams to work on is complex. Additionally, you might suffer a performance penalty for having to pack and unpack the streams before and after processing. But if we could find a simpler version of this approach, it might be worthwhile.

How will you handle stereo signals?

It’s probably a given that your synth will output stereo signals, so some or all of the signal processing chain will run in stereo. This basically means that you have to handle two separate audio streams, and you have to make some choices about how to make that happen.

Storage: Streams must be store either interleaved or non-interleaved.

Computation: How do you compute the two streams? Will you run the entire synth for the left side first, then the right? Will you run modules for the left side first, then the right? Or will you do the computations interleaved, because the streams are interleaved in storage?

No matter what you do, you will probably introduce this ubiquitous construct throughout your code:

for (uint32_t channel=0; channel<kNumChannels; channel++)
{
	// Insert single channel processing code here
}

The answer

Here is the answer to all of the above.

You should do your computations in 64-bit doubles using SSE. You should parallelize over the stereo signal, computing the two channels simoultaneously. You should handle denormals by disabling them in SSE.

So, we get the immediate disadvantage of doubling our memory bandwidth. However:

1. This significantly simplifies your processing code, because you don’t have to care about multiple channels anymore! You’re just computing one long stream of samples. You might be surprised that I list this as the first advantage - but try it and see. It is good!

2. Another simplification: You don’t have to worry about denormals anymore, because - by setting a few flags - you can set them to be flushed to zero in SSE! This is one advantage of doing your computations in SSE that the x87 FPU just can’t match.

3. You get the additional headroom of 64-bit doubles. This frees you up from having to worry about most numerical stability and precision issues. Just switch everything to run in doubles. It makes your code a little bigger, but we make up for that by making it more compressible² (which you’re doing if you care about code size, right?).

Try this. It’s a brilliantly simple way to work.

SSE!?

You might be thinking: “But Ralph, I thought you were all about simplicity. Now I have to care about 16-byte alignment, and write my processing code in SSE assembly?”

Yes. Yes you do. In the next article we’ll take a look at how to comfortably work with SSE in C++.